The other day I was tagged in a conversation between @WebBreacher and Nick Furneaux, where Nick asked whether it would be possible to calculate the position of a person within a photo. A quick search on the internet returned multiple blogs and websites with calculations based on the size of the camera sensor. But this would only work if an original and uncropped photo was used, preferably with the full EXIF data intact. That got me thinking: What if we only had access to an edited photo or video? Or media without any information about the equipment used?
After doing some research, it turned out that calculating the distance between an object in the photo and the camera with which the photo was taken is relatively straightforward. Nevertheless, three specific conditions have to be met:
- A second object must be in the photo of which the exact height is known
- The exact distance of this second object and the camera is known or can be determined accurately
- The exact height of the object with the unknown distance is known
What remains is some basic mathematics to determine the ratios of two triangles. Let’s have a look at the following scene, with the camera on the left capturing an image where two objects are visible. The first object is a car that is parked close by, of which we know the distance or can determine it, and the second object is a person at an unknown distance.
An Example

By adding in some lines for extra visibility, it turns out we are basically working with two right triangles, which in turn allows us to use geometry, so we can work out the distance by applying some mathematics. To see how that works, let’s apply it to the following case:
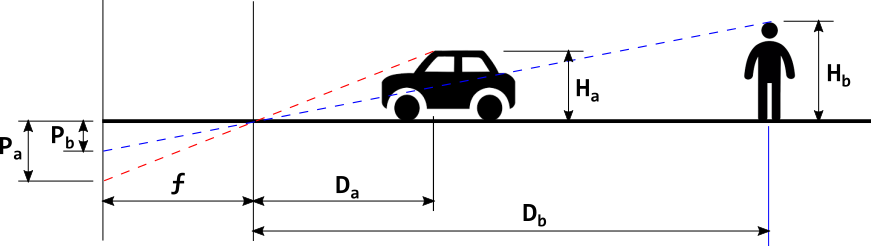
The line all the way on the left is the position of the imaginary camera or photograph we are examining. This can be the whole photograph, but can also be crop of a bigger scene. At the intersection of the lines we have an imaginary lens, just like in a regular camera. The distance between the lens and the sensor is called the focal length, or ƒ.
Then we have the two objects that we have in the photo. Finding the make and model of the car online makes it possible to determine the exact height (Ha). The distance between the car and the camera (Da) must be known but could even be recreated in a precise reenactment and measured afterwards, but sometimes it is simply impossible to visit the original location. As stated in the requirements before, we also need the height of the man (Hb), or at least a very good estimate. To determine how far away he was when the photo was taken, we are going to do some basic geometric calculations on these two right triangles.

Since the triangles on the left side of the lens have the same ratios as the triangles on the right, and we can calculate the value of ƒ, we can use that information to calculate any unknown side of any triangle on the right, for instance an unknown height or distance. We can determine the height of the triangles on the left in pixels, by simply measuring it in any image editor. Let’s first look at the ratio of the first triangle, which can be expressed through this small equation:
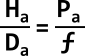
The fictive focal length — which is the same for both triangles — can be found by dividing the distance by the height of our reference object and multiply it by the height in pixels of that same object on the photo. That translates to this:
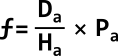
If we need to find the distance to the other object — the man in our example — we first need to rewrite the formula so we can calculate the unknown. This will result in the following:
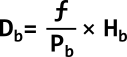
Since we already had a way to find the fictive focal length, we can substitute ƒ, so we get:
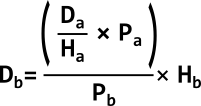
In case you want to automate the somehow in Excel, and you are confused with the brackets, another way of writing it down in a single line, is as follows. In this formula the quotient of the two ratios is multiplied by the known distance to find the unknown value:

Now all we need to do is fill in all the numbers we have. You don’t have to think about what unit you need, since we will only be working with the numbers itself. So you can use feet, metres or even kilometres, it will all work as long as you remember which unit you initially used for the calculations and you keep both distances in the same unit of measurement.
So let’s assume the car has a height of 1.4m at the measured spot on the roof, and this spot is exactly 5m away from us. We also know the person has a height of 1.8m. When we measure the pixels in the photograph, we find that the car has a height of 175 pixels (Pa) and the man has a height of 85 pixels (Pb).
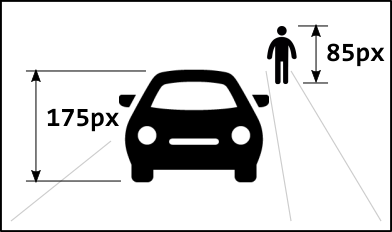
Now we can start filling in the formula as follows and will give us the distance of the man to the camera being 13.24m.
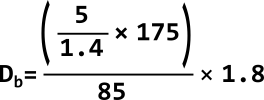
There are cases where this can be calculated or verified via different techniques, but when it is not possible to use any other information to calculate a distance, then this is a technique that can be used. The basics are extremely simple to grasp and everybody who had basic geometry in high school should be able to apply this to any given situation. The same principle can be used to determine the exact height of an object, but then we do need to know how how far away this object was when a photo or video was shot.
Use Cases and Final Thoughts
Some use cases I can think of are forensic investigations where objects or subjects have to be positioned precisely within a certain space, to get a better understanding of the distances between each of these. This can be the precise location of a person to determine someone was near enough for a specific action, like throwing a Molotov cocktail to name an example. Using the same principle to determine the height of a person accurately can be of use when a crime was captured by CCTV for instance.
Determining the exact location of the cameraman and the ‘known’ object can be a bit difficult sometimes, but within a video that turns left and right, one can for instance look for indications of the exact location of the cameraman. Think about paving tiles that can be measured to obtain the the distance with reasonably good accuracy. For photographs there are other techniques to triangulate the exact position of the cameraman, but that is a whole different topic for a whole different blog post. Another possibility is to go to the original site and recreate the scene, paying close attention to the correct focal lengths, lens distortion et cetera. And if it is not possible to measure it accurately, one can make an educated guess. The only issue with guessing is, that the accuracy will reduce when the distance between the two objects get larger.
To give an example, I applied the above to a photo of a person 3m away from me, with a large structure in the background at a calculated distance of around 650m. When changing the distance from 3 to 2.5m it was off by about 100m. So remember, if the distance between the two objects is extremely large, you have to make sure the known distance is as accurate as possible. Usually the known distance is the one close-by, and therefore the margin of error will be amplified when calculating the other distance.
One more thing about lens distortions, with certain smaller focal lengths it is possible that the sides of an image are warped extremely. A good example are fish eye lenses, and this can be problematic. In case the photo of interest has some form of distortion, I would advise to first ‘straighten’ it with a good photo editor. One of my ‘go-to-tools’ for this is Adobe Photoshop, but there are probably good alternatives out there.
It might seem that these are a lot of requirements, but it isn’t as bad as it looks. Just make sure you have a straight photo, correct measurements and a clear definition of what you want to know. The maths are simple and can be applied by everyone that needs it. And after doing a bit of research, I found out that this technique isn’t really new. A bit of digging for some keywords gave me a publication from 1980 called ‘Visual Resource Management: Visual simulation techniques‘ where on page 37 they write about ‘scaling techniqures’, which is exactly what is described in this blog.

So there we have it, knowledge that is thousands of years old can be used to determine a distance of an object that is shown in a digital image on your computer.
Well, here you go Nick!

